RENTREE DE CHAPMAN

	CONTENU : Mis à jour 12 janvier 1999, sept 2011 I Hypothèses de calcul II Notations et fonction de Chapman Figure | Fonction de Chapman | Calcul de la fonction de Chapman III Résultats de Chapman Evolution de l'altitude Evolution des autres paramètres  NB : le téléchargement regroupe 4 cours sur la rentrée Rentrée d'Allen - Rentrée de Chapman - Déorbitation Arc atmosphérique

Vous avez peut être déjà consulté la théorie d'Allen et êtes au courant de la manœuvre de déorbitation qui précède la traversée des couches atmosphériques terrestres ou éventuellement martienne.

Pour avoir quelques idées précises sur l'évolution des paramètres de rentrée, position, vitesse, accélération, traînée,… Chapman, au prix de simplifications bien justifiées, a mis au point une méthode de calcul adaptée aux angles de rentrée réduits ( <6°) et surtout aux rentrées planées utilisant une portance. L'avantage de la méthode est de s'appliquer à des rentrées sur d'autres planètes.

I HYPOTHESES DE CALCUL :

Tout ce cours est fourni avec des données relatives à la planète terre, mais la théorie peut s'adapter à d'autres planètes, notamment Mars qui est candidate à une descente par freinage atmosphérique

1°) Modélisation de la masse volumique de l'air. Une loi exponentielle est adoptée de la forme ci dessous, où Z désigne l'altitude sol et b une constante:

Pour Mars: consulter le projet de rentrée ou un site adéquat., les constantes ro et b doivent être adaptées

2°) La rentrée étant très largement hypersonique, les coefficients aérodynamiques de traînée Cx et de portance Cz sont constants.

3°) La théorie complète celle d'Allen qui n'est valable que pour des angles de rentrée supérieurs à 6°, celle de Chapman impose de petits angles de rentrée inférieurs à 6°.

4°) Contrairement aux calculs d'Allen, la pesanteur est prise en compte mais sa variation en fonction de l'altitude ne l'est pas.

5°) La terre( ou une autre planète) est supposée immobile.

II NOTATIONS ET FONCTION Y(x) DE CHAPMAN :

Nous n'allons pas refaire tous les calculs de Chapman, renvoyant le lecteur aux ouvrages spécialisés, en particulier Re-entry and Planetary Entry, Physics and technology by W.H.T LOH, SPRINGER- Verlag New-York 1968.

Indiquons simplement que Chapman part de la loi fondamentale de la mécanique, en projection sur les axes des coordonnées polaires associées au mouvement.

1°) FIGURE ET NOTATIONS :

On note avec en appui la figure:

• V la vitesse courante, g la pente, positive si V est sous l'horizontale
• u la vitesse orthoradiale ou encore horizontale u = Vcosg, uo est la vitesse d'orbitation circulaire à l'altitude où se trouve l'engin.
• f la finesse f = Rz / Rx = Cz / Cx, avec Cx coefficient de traînée et Cz celui de portance
• Rm 3460 km ( valeur à adapter pour une autre planète) désignera la valeur moyenne du rayon vecteur entre l'entrée et le sol.
• S est la surface de référence des calculs aérodynamiques et M la masse du corps de rentrée.
• M est la masse du corps de rentrée

NB : La théorie faisant- appel à des simplifications, n'est valable que sous la condition :

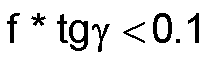
2°) FONCTION x ---> Y(x) DE CHAPMAN :

Chapman définit une variable x sans dimension et une fonction Y(x) également sans dimension, de la manière suivante

3°) COMMENT TABULER Y(x) ?

a. Equation différentielle vérifiée par Y(x) :

Chapman, après des calculs non explicités, montre que Y(x) vérifie une équation différentielle d'ordre 2 :

b) Conditions initiales et tabulation de Y(x):

Il faut tout d'abord calculer la manœuvre de déorbitation. Ceci donnera donc x_o = V_eo cosg_eo . De même, avec l'altitude initiale Ze = 80 km( valeur à adapter pour une autre planète), on peut calculer la valeur de Y(xo), et ainsi la dérivée initiale Y'(xo)

Les calculs se ramènent alors à une programmation de calculs numériques, fournissant une tabulation de Y(x) et naturellement de sa dérivée Y'(x).

III RESULTATS DE CHAPMAN :

1°) EVOLUTION DE L'ALTITUDE :

La connaissance de Y(x) et le choix de la finesse permettent le calcul de tous les paramètres de rentrée par :

relation qui montre de manière très explicite, trois termes:

• le premier dépendant uniquement du choix de la rentrée, altitude, vitesse, angle et finesse
• le deuxième ne dépendant que de la forme du corps de rentrée, il montre en particulier et on y trouvera une confirmation des calculs de Allen, que la forme n'intervient que sous forme d'un décalage d'altitude.
• le troisième représente la part de la planète, avec ses caractéristiques propres, rayon moyen atmosphérique et modélisation de la masse volumique de l'atmosphère.

2°) AUTRES PARAMETRES:

a. Angle de rentrée, qu'il faut surveiller, car ne devant pas dépasser 10°, pour que la théorie reste valide.

b. La traînée qui se calcule par rapport au poids: mg.

ATTENTION: g est l'accélération de la gravitation de la planète, donc c'est une valeur à adapter à chaque cas de rentrée.

et naturellement, la portance grâce à la finesse.

c. La norme V de la vitesse, la décélération horizontale G

NB : Il est bien dit la décélération horizontale, c'est à dire la composante orthoradiale de l'accélération, due uniquement à la traînée. D'ailleurs G = Rxcosg/m.

ATTENTION: g est l'accélération de la gravitation de la planète, donc c'est une valeur à adapter à chaque cas de rentrée.

Si l'on veut réellement les 2 composantes de l'accélération, signes compris :

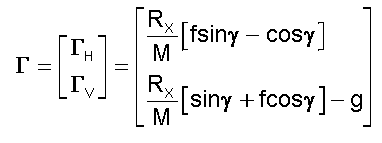
On constatera que la composante horizontale ne diffère de celle plus simple indiquée plus haut que de 10% au maximum, vue la condition imposée par la théorie.

d. Le temps au cours de la rentrée, permettant de graduer la trajectoire.

ATTENTION: g est l'accélération de la gravitation de la planète, donc c'est une valeur à adapter à chaque cas de rentrée.

e. La distance sol parcourue depuis le point d'entrée :

3°) COMMENTAIRES:

Une comparaison avec d'autres calculs non simplifiés, révélera naturellement quelques divergences normales dans les résultats. La théorie de Chapman donne cependant de bons résultats, au prix d'une modélisation simple de l'atmosphère d'une planète.

Guiziou Robert décembre 2001, sept 2011